Update 2017-02-18: The XP/level curve I was using in the first iteration of this post was based on a previous version of the game. The current XP curve paints a very different picture. I have updated the graphs.

Since it was bugging me, I decided to visualize some of the relationships between playtime, paragon, greater rifts and power levels.

Baseline assumptions

Since we have to use some reference point, I’ll offer my own gear. For ease of comparison, I’m going to ignore everything below paragon 800 and use that as my “starting point”.

I’m pretty decently equipped, and using only the points available to me at paragon 800 I have somewhere in the ballpark of 15,000 dex and 10,000 additional bonus armor from gear:

baseDex = 15000
baseArmor = 10000

At this gear level and no further paragon points, I can do something like 180 billion XP/hour on a good day, speed-farming GR75 or so. (solo)

baseXph = 180

In terms of progress, with this gear level, I can do something like GR 90.

baseRiftLevel = 90

Basic relationships

In order to establish some common relationships, a few basic definitions:

Main stat versus paragon level

This is pretty trivial. Each paragon level is 5 dex more.

dexPara(paraLevel) = baseDex + 5 * (paraLevel - 800)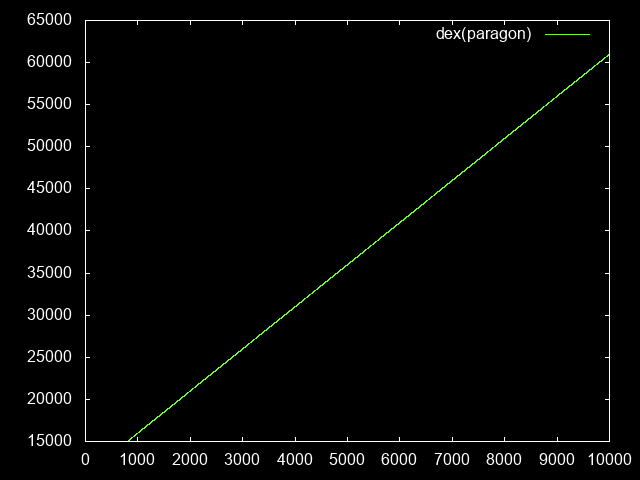

Main stat versus damage output

Each point of dexterity increases my damage by 1%, stacking additively with itself. For simplicity, we’ll normalize it so that ‘1’ is my baseline damage.

damageDex(dex) = (1 + dex / 100) / (1 + baseDex / 100)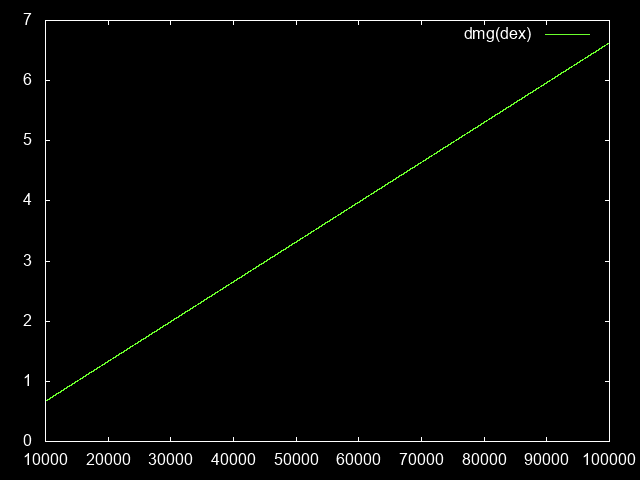

Main stat versus damage mitigation

Twice as much armor = Half as much damage, so we can just calculate this in terms of the baseline. Again, ‘1’ means my baseline damage mitigation.

toughnessDex(dex) = (baseArmor + dex) / (baseArmor + baseDex)
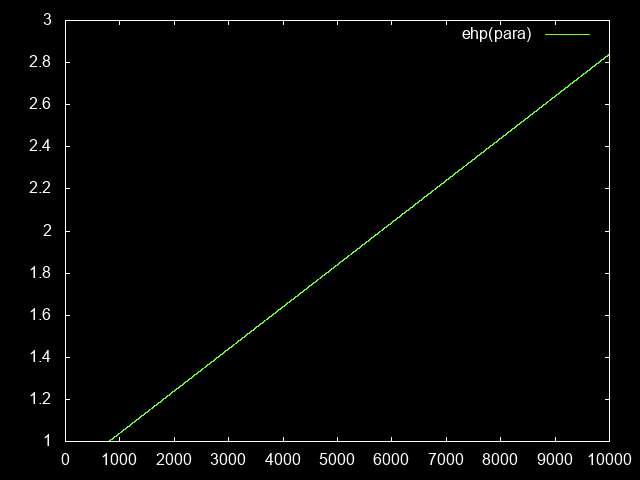
toughnessPara(paraLevel) = toughnessDex(dexPara(paraLevel))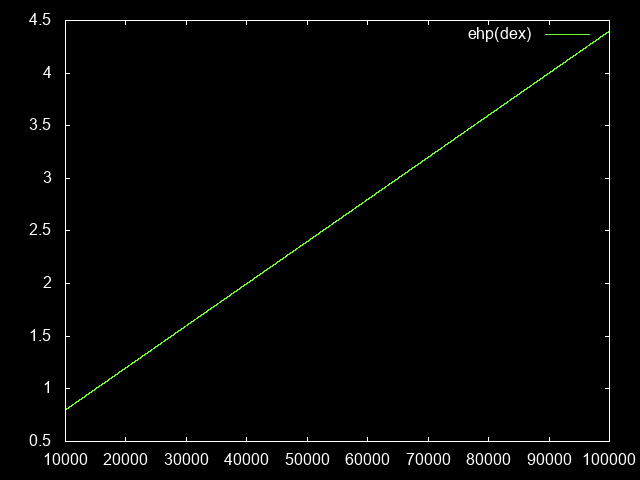

GR level versus mob HP

Each additional GR level increases mob HP by 17%. We can use my baseline as a reference point for how much damage you need to be dealing per GR level, and scale it from there.

riftLevelDamage(damage) = baseRiftLevel + logBase 1.17 damage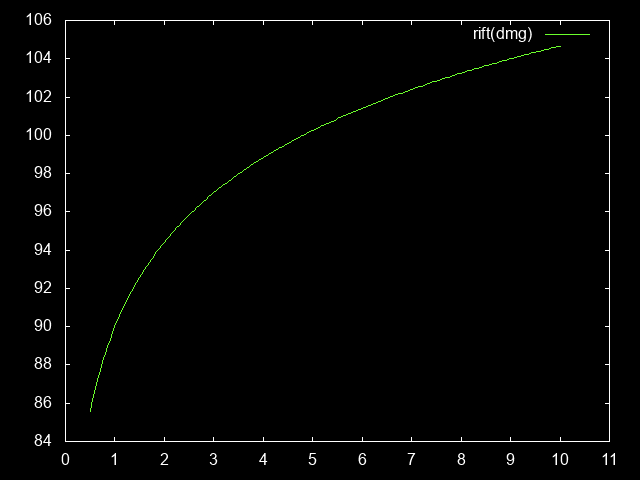

Mob damage versus GR level

For each level above GR70, mobs deal 2.34% more damage. So the increase in toughness required per GR level is as follows:

incomingDamage(riftLevel) = 1.0234 ** (riftLevel - baseRiftLevel)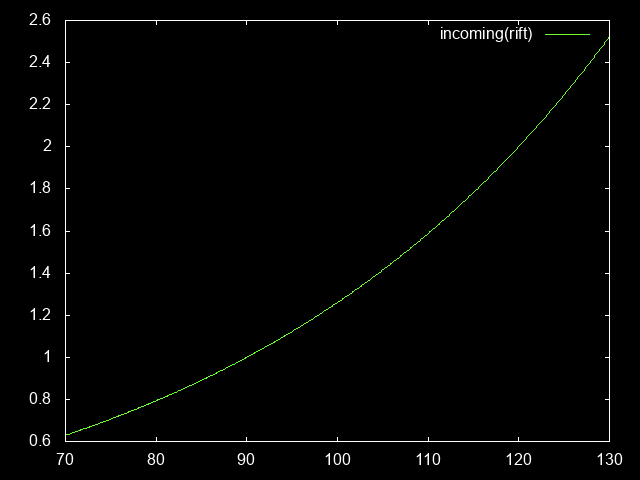

Derived functions

Now we’re ready to look at the first set of relationships between these curves:

Damage output versus paragon level

More paragon = more dex = more damage. Simple enough. Plug one into the other:

damagePara(paraLevel) = damageDex(dexPara(paraLevel))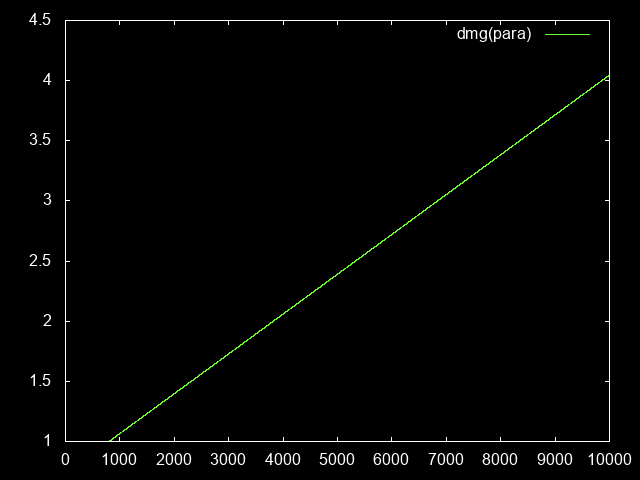

GR level versus paragon level

Take the previous curve and plug it into the damage <-> GR level curve:

riftLevelPara(paraLevel) = riftLevelDamage(damagePara(paraLevel))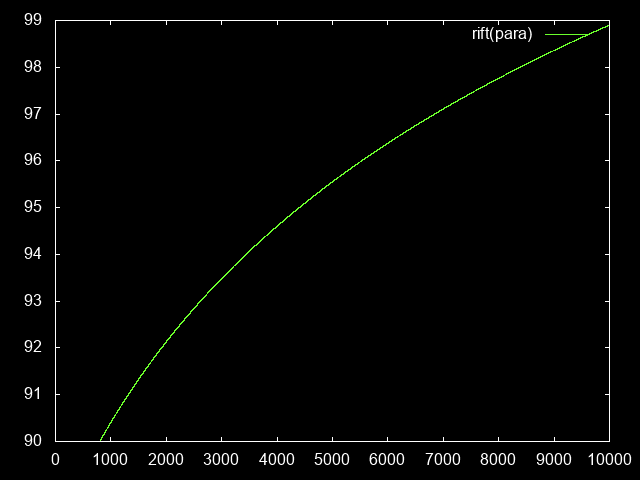

Incoming damage at this paragon level

Of course, at this higher GR level, we’ll also be receiving more incoming damage.

incomingDamageRaw(paraLevel) = incomingDamage(riftLevelPara(paraLevel))
incomingDamageEff(paraLevel) = incomingDamageRaw(paraLevel) / toughnessPara(paraLevel)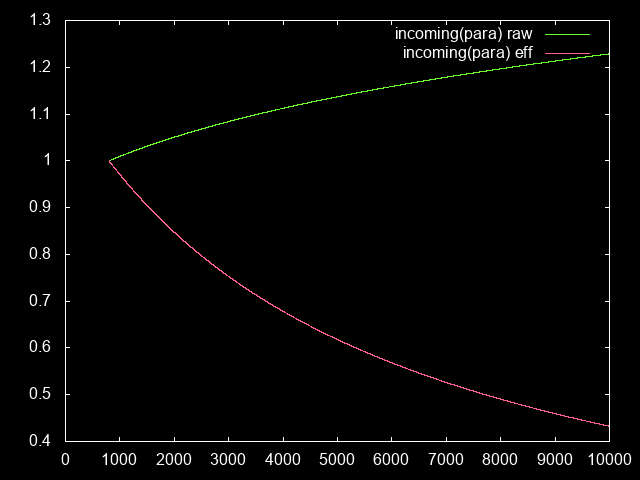

Even though the raw damage increase is going up, the actual effective damage (relative to how much armor we gain) is going down; meaning we actually have an easier time surviving than in the lower GR90.

Note: This means that, technically, we could swap out a 50% defensive modifier (e.g. crystal fist) for an offensive piece of gear at para 9000, and still survive. But we’ll ignore this effect for now, for the sake of moving on to more interesting things.

The time axis

All this is well and good, but my main interest lies in how all of these stats correlate with actual playtime. So first, we need to figure out how XP scaling works.

As of patch 2.4.2 (S8), the paragon curve above p800 is subdivided into two halves: There’s a p800-2250 segment, which increases linearly starting from 23 (billion) and ending at 200. After that, it increases quadratically, gaining by 102 thousand per level.

xpLevel(paraLevel)
  | paraLevel <= 2250 = lerp (800, 23) (2250, 200)
  | otherwise         = 200 + 0.229602 * bonusPara + 0.000051 * bonusPara^2

  where lerp (a,x) (b,y) = x + (paraLevel - a) / (b - a) * (y - x)
        bonusPara        = paraLevel - 2250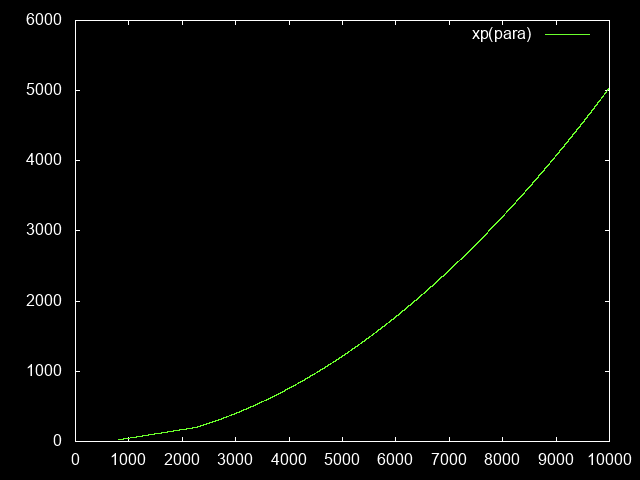

XP/hour versus paragon level

Obviously, we have to take into account the effects of higher paragon levels allowing you to farm more quickly. So first of all, we need to know how much XP/hour we would expect at each paragon level. To do this, let’s assume we continue farming on the same GR level, but clear the rift more quickly. (This is more or less equivalent to farming at a higher GR level but more slowly, close enough for our purposes)

xphPara(paraLevel) = baseXph * damagePara(paraLevel)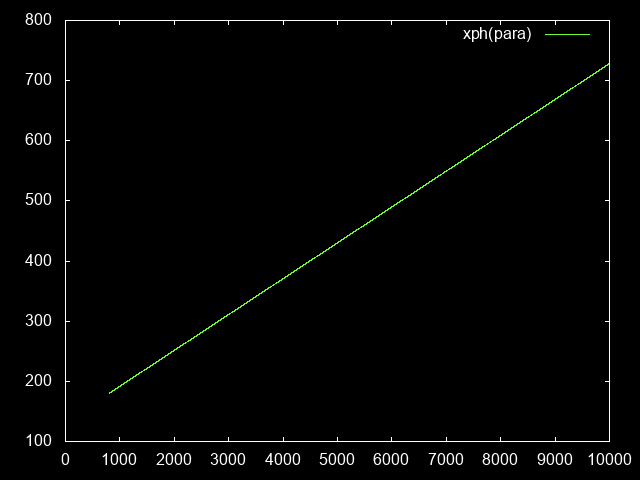

Time needed per paragon level

Here’s an interesting aside that will be useful: How many minutes does a single paragon level take?

hoursPerPara(paraLevel) = xpLevel(paraLevel) / xphPara(paraLevel)
minPerPara(paraLevel) = hoursPerPara(paraLevel) * 60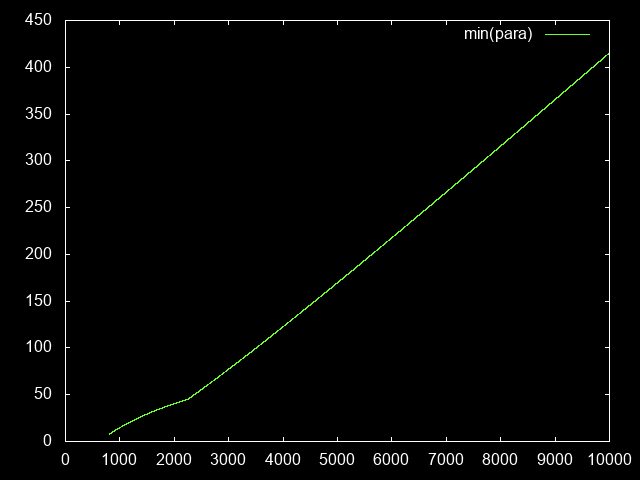

Paragon level per hour of playtime

To know, therefore, how many minutes/hours of farming time we need to reach a certain total paragon level, we can accumulate the previous curve over time:

paraHours = go 800 0 where
  go level hours
    | level > 10000 = []
    | otherwise     = (hours, level) : go (level+1) (hours + hoursPerPara(level))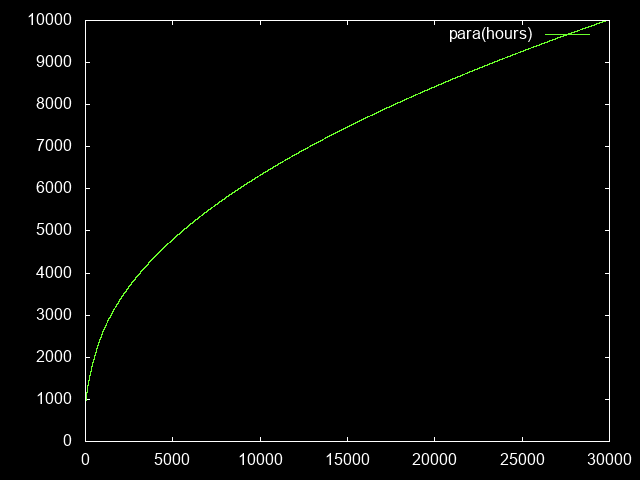

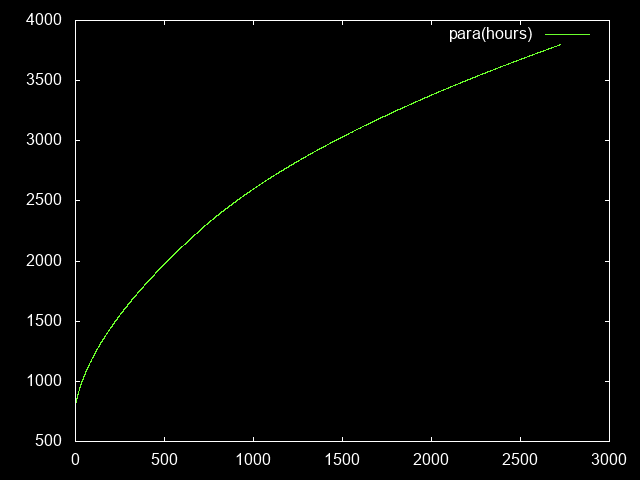
To reach paragon 10,000, one has to play for about 30k hours ≈ 3-4 ingame years.

GR level per hour of playtime

Finally, since this is the result I was ultimately interested in, the GR level this translates to, as a function of the time spent grinding:

riftHours = [ (hours, riftLevelPara(paraLevel)) | (hours, paraLevel) <- paraHours ]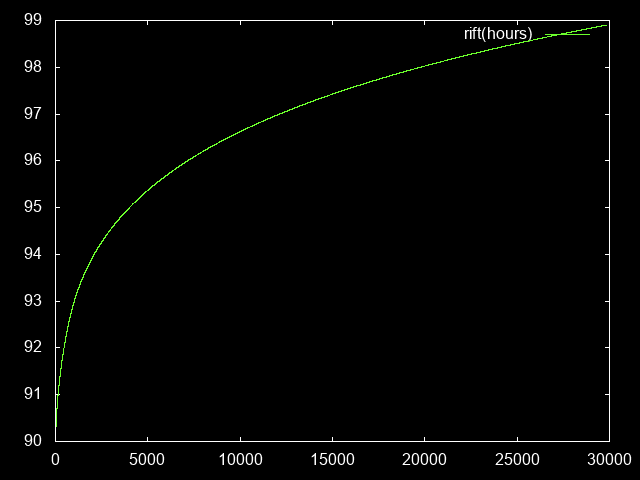

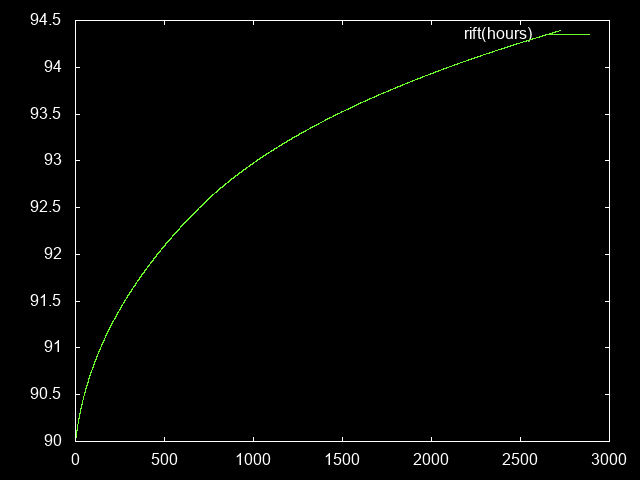
Summary

In summary, how much benefit you get out of the paragon system slows down over time, culminating in the point where you need to invest exponentially increasing amounts of gametime to reach the next GR level.

Might be slightly skewed towards the upper end due to the effects of decreasing incoming damage, but I don’t have a good model for that.

If there’s something I’m unsure about, it’s how your XP/hour increases as a function of your paragon level - it seems like 700b XP/hr might be over-estimating things at the high end. Nonetheless, based on figures I’m seeing from paragon ~4000 players, it seems to match the curve so far.